Генерація вищих гармонік
Генерацією вищих гармонік (англійська абревіатура HHG) називається процес випромінювання електромагнітних хвиль зразком-мішенню (газом, плазмою, твердим тілом або рідиною) при опроміненні лазерним імпульсом на частоті, кратній (принаймні у п'ять разів) частоті цього імпульсу. Генерація вищих гармонік є методом створення високочастотних джерел випромінювання, а завдяки когерентній природі цього процесу генерація вищих гармонік використовується в атосекундній фізиці.
Пертурбаційна генерація гармонік це процес, в якому лазер із частотою ω та енергією фотона ħω використовується для створення світла з іншою частотою. Нові частоти nω є кратними початковій частоті світла. Уперше цей процес відкрили 1961 року Франкен зі співробітниками[1], використовуючи рубіновий лазер та кристалічний кварц як нелінійне середовище.
Генерація гармонік у твердотільних діелектриках добре зрозуміла й широко використовується в сучасній лазерній фізиці (дивіться генерація другої гармоніки). У 1967 Нью та інші уперше спостерігали генерацію третьої гармоніки в газах[2]. У моноатомних газах можна отримати тільки гармоніки непарної кратності, як випливає з міркувань симетрії. У режимі слабкого поля інтенсивність збуджених гармонік швидко зменшується з порядком[3]. Це можна зрозуміти як поглинання атомом n фотонів, а потім випромінювання одного більшої частоти. Ймовірність поглинання n фотонів падає з ростом n, що й зумовлює швидке зменшення інтенсивності гармонік.
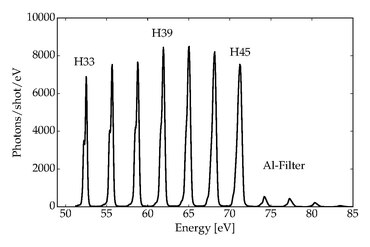
Уперше генерація вищих гармонік спостерігалася в 1977 у взаємодії потужного імпульсу CO2 лазера з плазмою, утвореною з твердотільної мішені[4]. Генерацію вищих гармонік у газах, найпоширеніше сьогодні застосування, уперше спостерігали Макферсон зі співробітниками в 1987[5], а пізніше Феррей та інші в 1988[6] з несподіваним результатом: інтенсивність вищих гармонік очікувано спадала при малих порядках, але далі спостерігалося плато, на якому інтенсивність гармонік залишалася постійною для багатьох порядків[7]. Плато гармонік покриває діапазон у сотню електронвольт аж до м'якого рентгену[8]. Воно різко обривається в місці, яке називають обрізанням гармонік.
Високі гармоніки мають ряд цікавих особливостей. Вони є джерелом далекого ультрафіолету й м'якого рентгену, джерелом, що поміщається на столі, й частоту якого можна змінювати, синхронізоване з лазером, а період між імпульсами той же, що й у лазера. Частота обрізання гармонік лінійно залежить від потужності лазера до певної потужності насичення Isat, при якій генерація гармонік припиняється[9]. Потужність насичення можна змінити вибором легшого інертного газу ціною втрати ефективності конверсії, тож існує певний оптимум залежно від енергії бажаного фотона.
Генерація високих гармонік сильно залежить від поля початкового лазера, і як наслідок гармоніки мають схожі часові й просторові когерентні властивості[10]. Високі гармоніки часто генерують імпульсами з тривалістю меншою, ніж тривалість початкового імпульсу[11]. Причина цього — нелінійність процесу, узгодження фаз та іонізація. Часто гармонки генеруються у дуже маленькому часовому вікні, коли виконуються умови узгодження фаз. Виснаження активного середовища внаслідок іонізації також означає, що генерація високих гармонік в основному зосереджена на передньому краю початкового лазерного імпульсу[12].
Високі гармоніки випромінюються колінеарно до вихідного лазерного променя і можуть бути дуже тісно обмеженими просторово, іноді з меншою розбіжністю, ніж основне поле, й мають профіль, близький до гаусового[13].
Максимальна енергія фотона, якої можна добитися методом генерації високих гармонік, визначається обрізанням плато генерації. Її можна розрахувати класично, аналізуючи максимальну енергію, якої може набути вибитий при іонізації електрон в електричному полі лазера. Енергія обрізання задається формулою[14]:
де Up — пондеромоторна енергія лазерного поля, а Ip — енергія іонізації.
Формула для енергії обрізання виведена з напівкласичних міркувань. Спочатку електрон, поки він тунелює, відриваючись від свого атома, розглядається квантовомеханічно, але надалі для опису його динаміки використовують класичний підхід. Вважається, що електрон народжується у вакуумі з нульовою швидкістю, а потім прискорюється електричним полем лазерного променя.
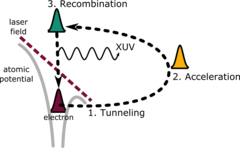
На половині оптичного циклу після іонізації електрони змінюють напрям руху зі зміною електричного поля, й прискориться в напрямку власного ядра. Повернувшись до нього він випромінюватиме щось на зразок гальмівного випромінювання в процесі рекомбінації з поверненням до основного стану. Це опис відомий під назвою рекомбінаційної моделі[15].
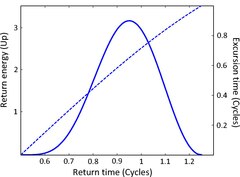
Оскільки частота рекомбінаційного випромінювання залежить як від кінетичної енергії, так і від потенціалу іонізації, на різних стадіях рекомбінації випромінювання відбувається на різних частотах (тобто випромінюваний імпульс чирпований). Щобільше, для кожної частоти є два відповідних часи рекомбінації. Ми називаємо ці дві траєкторії короткою траєкторією (першою) і довгою траєкторією.
Цікаві обмеження процесу генерації вищих гармонік, пояснені цією моделлю, демонструють, що генерація відбувається тільки тоді, коли поле лазера лінійно поляризоване. Еліптична поляризація змушує електрон пролетіти повз ядра. Мовою квантової механіки це означає зменшення перекриття хвильових функцій електрона при поверненні та ядра. Явище спостерігалося експериментально як швидке зменшення інтенсивності згенерованих гармонік зі збільшенням еліптичності[16].
Як і в кожному нелінійному процесі при генерації вищих гармонік у газі узгодження фаз відіграє важливу роль. У геометрії вільного фокусування існують чотири причини неузгодження хвильових векторів: нейтральна дисперсія, плазмова дисперсія фаза Гуї та дипольна фаза. [17][18].
- ↑ P. A. Franken, A. E. Hill, C. W. Peters, and G. Weinreich, Phys. Rev. Lett. 7, 118 (1961).
- ↑ New, G. H. C.; Ward, J. F. (1967). Optical Third-Harmonic Generation in Gases. Phys. Rev. Lett. 19 (10): 556—559. Bibcode:1967PhRvL..19..556N. doi:10.1103/physrevlett.19.556.
- ↑ J. Wildenauer, Journal of Applied Physics 62, 41 (1987).
- ↑ Burnett, N. H. та ін. (1977). Harmonic generation in CO2 laser target interaction. Appl. Phys. Lett. 31 (3): 172—174. Bibcode:1977ApPhL..31..172B. doi:10.1063/1.89628.
- ↑ McPherson, A. та ін. (1987). Studies of multiphoton production of vacuum-ultraviolet radiation in the rare gases. JOSA B. 4 (4): 595. Bibcode:1987JOSAB...4..595M. doi:10.1364/JOSAB.4.000595.
- ↑ Ferray, M. та ін. (1988). Multiple-harmonic conversion of 1064 nm radiation in rare gases. Journal of Physics B: Atomic, Molecular and Optical Physics. 21 (3): L31. Bibcode:1988JPhB...21L..31F. doi:10.1088/0953-4075/21/3/001. S2CID 250827054.
- ↑ Li, X. F.; L'Huillier, A.; Ferray, M.; Lompre, L. A.; Mainfray, G. (1989). Multiple-harmonic generation in rare gases at high laser intensity. Physical Review A. 39 (11): 5751—5761. Bibcode:1989PhRvA..39.5751L. doi:10.1103/physreva.39.5751. PMID 9901157.
- ↑ Seres, J. та ін. (2005). Laser technology: Source of coherent kiloelectronvolt X-rays. Nature. 433 (7026): 596. Bibcode:2005Natur.433..596S. doi:10.1038/433596a. PMID 15703738. S2CID 4425428.
- ↑ Brabec, T.; Krausz, F. (2000). Intense few-cycle laser fields: Frontiers of nonlinear optics. Reviews of Modern Physics. 72 (2): 545—591. Bibcode:2000RvMP...72..545B. doi:10.1103/revmodphys.72.545.
- ↑ L'Huillier, A.; Schafer, K. J.; Kulander, K. C. (1991). Theoretical aspects of intense field harmonic generation. Journal of Physics B: Atomic, Molecular and Optical Physics. 24 (15): 3315—3341. Bibcode:1991JPhB...24.3315L. doi:10.1088/0953-4075/24/15/004. S2CID 250751106.
- ↑ Streaking of 43-attosecond soft-X-ray pulses generated by a passively CEP-stable mid-infrared, https://doi.org/10.1364/OE.25.027506
- ↑ Schafer, K. J.; Kulander, K. C. (1997). High Harmonic Generation from Ultrafast Pump Lasers. Physical Review Letters. 78 (4): 638—641. Bibcode:1997PhRvL..78..638S. doi:10.1103/physrevlett.78.638.
- ↑ Tisch, J. W. G. та ін. (1994). Angularly resolved high-order harmonic generation in helium. Physical Review A. 49 (1): R28—R31. Bibcode:1994PhRvA..49...28T. doi:10.1103/physreva.49.r28. PMID 9910285.
- ↑ Krause, Jeffrey L.; Schafer, Kenneth J.; Kulander, Kenneth C. (1992). High-order harmonic generation from atoms and ions in the high intensity regime. Physical Review Letters. 68 (24): 3535—3538. Bibcode:1992PhRvL..68.3535K. doi:10.1103/PhysRevLett.68.3535. PMID 10045729.
- ↑ Corkum, P. B. (1993). Plasma perspective on strong field multiphoton ionization. Physical Review Letters. 71 (13): 1994—1997. Bibcode:1993PhRvL..71.1994C. doi:10.1103/physrevlett.71.1994. PMID 10054556. S2CID 29947935.
- ↑ Dietrich, P.; Burnett, N. H.; Ivanov, M.; Corkum, P. B. (1994). High-harmonic generation and correlated two-electron multiphoton ionization with elliptically polarized light. Physical Review A. 50 (5): R3585—R3588. Bibcode:1994PhRvA..50.3585D. doi:10.1103/physreva.50.r3585. PMID 9911439.
- ↑ Altucci, C.; Starczewski, T.; Mevel, E.; Wahlström, C.-G.; Carré, B.; L'Huillier, A. (1996). Influence of atomic density in high-order harmonic generation. J. Opt. Soc. Am. B. 13 (1): 148—156. Bibcode:1996JOSAB..13..148A. doi:10.1364/JOSAB.13.000148.
- ↑ Pascal, Salieres; L'Huillier, Anne; Lewenstein, Maciej (1995). Coherence control of high-order harmonics (PDF). Physical Review Letters. 74 (19): 3776—3779. Bibcode:1995PhRvL..74.3776S. doi:10.1103/physrevlett.74.3776. PMID 10058294. S2CID 35091499.
